문제 설명

지도를 종이에 인쇄하려고 한다. 그런데 종이의 크기는 무한하지 않고, $w,h$로 주어진다. 이제 지도 하나를 여러 개의 종이에 걸쳐 인쇄하려고 하는데, 이 때 필요한 종이의 최소 개수를 구하는 문제이다.

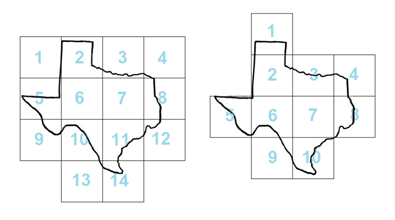
지도가 저렇게 되어 있으면 최소 10장으로 출력할 수 있다.

풀이

일단 이 문제는 종이의 시작 위치를 어떻게 정할지 라고 생각했다. 일단 종이를 무한히 두고, 그 중 그림이 그려지는 종이만 카운트하면 그게 종이의 필요한 개수라고 생각할 수 있다. 즉, 격자라고 생각할 수 있다. 그리고 격자의 중심을 이렇게 정의할 것이다. 만약 0,0에서 격자가 시작하고, 종이의 크기는 $w,h$이면 $(wk, hk_2) (k,k_2는 정수)$는 전부 격자의 중심이다.

일단 격자가 어떻게 놓여야 정답일지 생각해 보자. 격자의 중심 중 하나는 무조건 다각형에 붙어 있을 겻이다. 물론 안 붙어 있는 경우도 있지만, 붙어있는 경우가 없을 수는 없다. 안 붙어 있어도 종이 사용 개수는 똑같게 한 채로 조금씩 격자를 한 쪽으로 이동시키면 언젠가는 다각형과 만나기 때문이다. 그런데 이렇게 하나가 다각형에 붙어 있어도 사용하는 종이의 개수는 그대로인 채로 계속 움직일 수 있다. 어떤 경우에 완전히 고정되어서 못 움직일까? 격자의 중심 중 다른 하나가 다각형에 닿아있다면 이제 2군데가 다각형에 닿아있으니 미세하게 더 움직이지 못할 것이다. 어떻게 움직여도 종이 사용 개수가 달라질 것이다. 그런데 이런 경우 말고 또 있다. 이런 경우를 생각해 보자

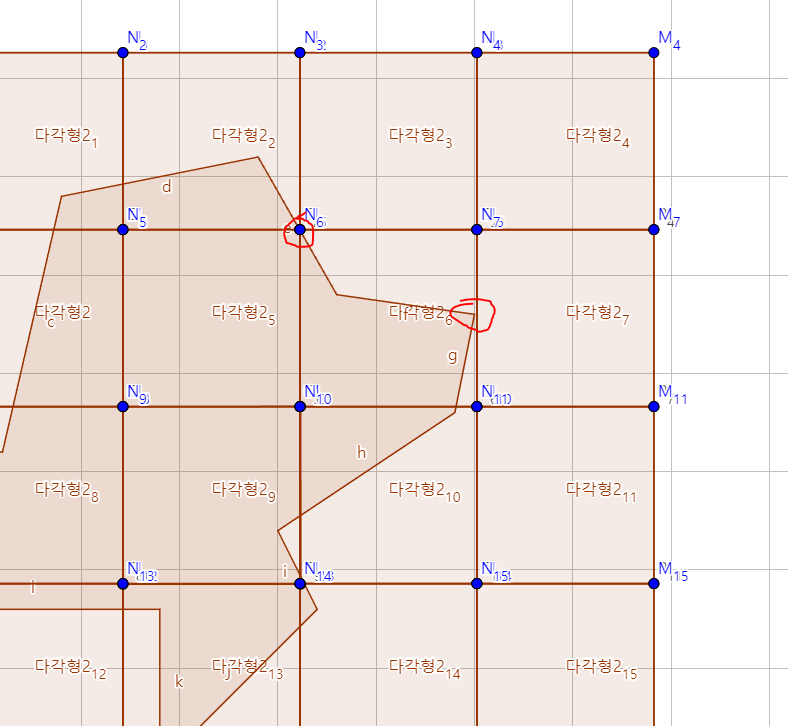
이런 경우 격자를 조금이라도 왼쪽으로 옮기려면, 점 $A$ 때문에 사용하는 종이의 개수가 달라 질 것이다. 따라서, 점이 아니라 이렇게 격자의 한 선분하고 부딪히는 경우도 고려해야 한다.

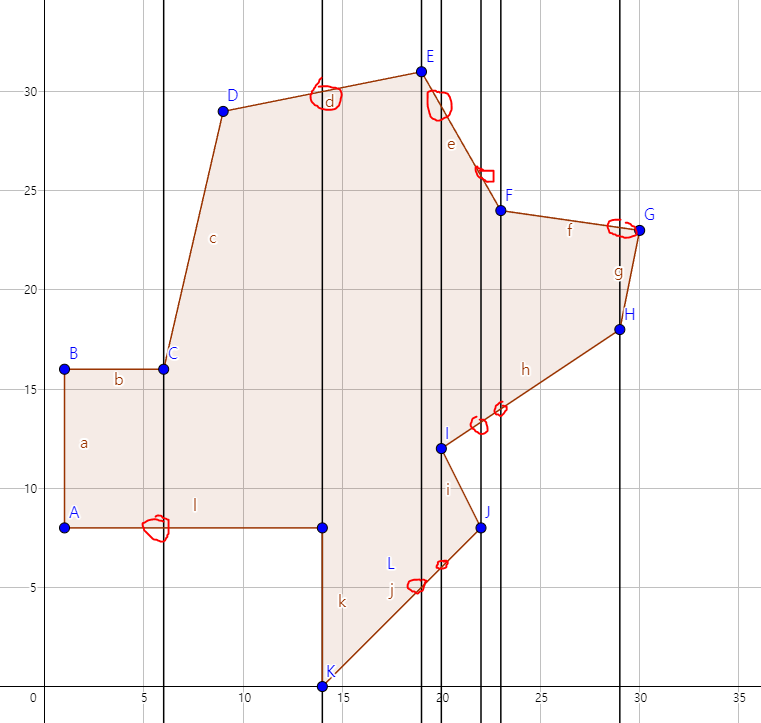
이렇게 표시된 점을 전부 보면 된다. 여기서는 x좌표에 대해서만 봤는데 y좌표에 대해서도 봐야 한다.

원래 이렇게 풀이 마무리 하려고 했는데, 첫번 째 경우인 두 점이 닿는 경우는 어떻게 구해야 하는지 정도만 더 써 보겠다. 첫번째 점을 $p_1$이라 하자. 그리고 두 번째 점을 $p_2$라 하자. 그러면 $p_1$이 정해졌으면, $p_2$는 어디 있을까?

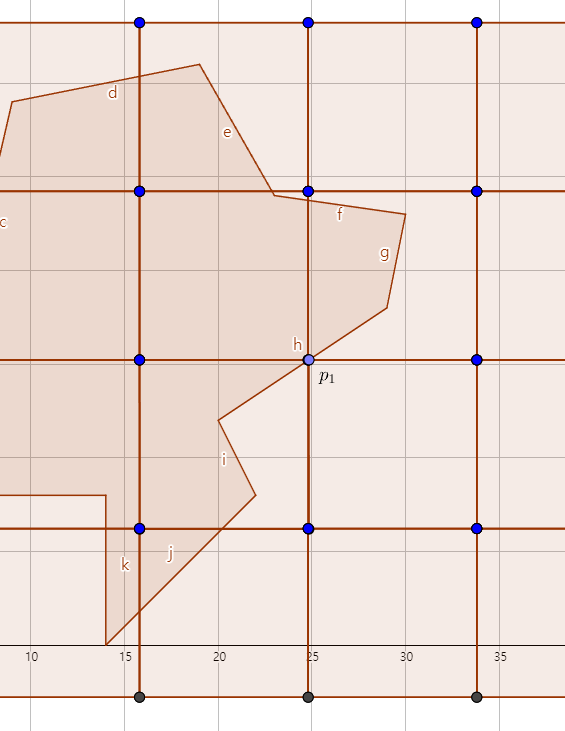
이런 식으로 저기 있는 $p_1$을 제외한 점들이 전부 $p_2$가 될 수 있을 것이다. 그런데 이 중, 다각형의 한 선분에 닿는 것만 찾아야 한다. 그리고 $p_1$이 조금씩 움직일 때 마다 가능한$p_2$도 전부 조금씩 움직여 봐야 한다. $p_1$은 다각형에 닿아 있어야 하기 때문에, $p_1$이 다각형의 테두리를 따라 움직인다고 하자. 여기서는 $a_1$에서 $a_2$를 향해 간다고 하자. 그러면 가능한 $p_2$도 전부 $p_1$과 같이 움직일 것이다. 즉, $\overline{a_1a_2}$를 평행이동 한 것이 $p_2$가 가능한 곳의 궤적이라 할 수 있다. 이제 이 것과 교차하는 다각형의 테두리가 있나 확인하고, 교차하면 그 점이 $p_2$이다. 여기서 $p_1$은 따로 확인 할 필요 없다. $p_1$이나 $p_2$나 둘 다 격자의 중심이라 할 수 있기 때문에 $p_2$를 기준으로 잡아도 된다.

여담

이 문제도 실수오차 문제가 있는데, 더 귀찮은건 결과값은 정수로 나와야 하고, 여러개를 정답으로 인정해주지 않는다는 거다.. 다각형이 $10^{-6}$만큼 종이 밖으로 나가도 정답은 같다는 것 때문에 오히려 더 풀기 귀찮았던 것 같다.