문제 설명

Simple Polygon이 주어진다. 그러면 다각형의 내부에 한 점을 찍는다. 만약 이 점에서 모든 정점까지 시계방향만으로 꺾으며 가도 갈 수 있으면 이를 재미있는 점이라 한다. 재미있는 점이 될수 있는 곳은 무수히 많을 것이다. (물론 없을수도 있다.) 이 재미있는 점의 집합의 영역의 넓이를 구하는 문제이다.

풀이

한 점에서 모든 정점에 시계방향으로만 꺾으며 도달할 수 있어야 한다는 뜻은, 반대로 말하면 모든 정점에서 시작해서 반시계방향으로만 꺾으며 도달할 수 있어야 한다. 그러면 한 정점에서 도달할 수 있는 영역을 먼저 구해보도록 하자. (사실 다른 점의 영역도 일부 신경 쓸 것인데 이는 뒤에서 설명하겠다.)

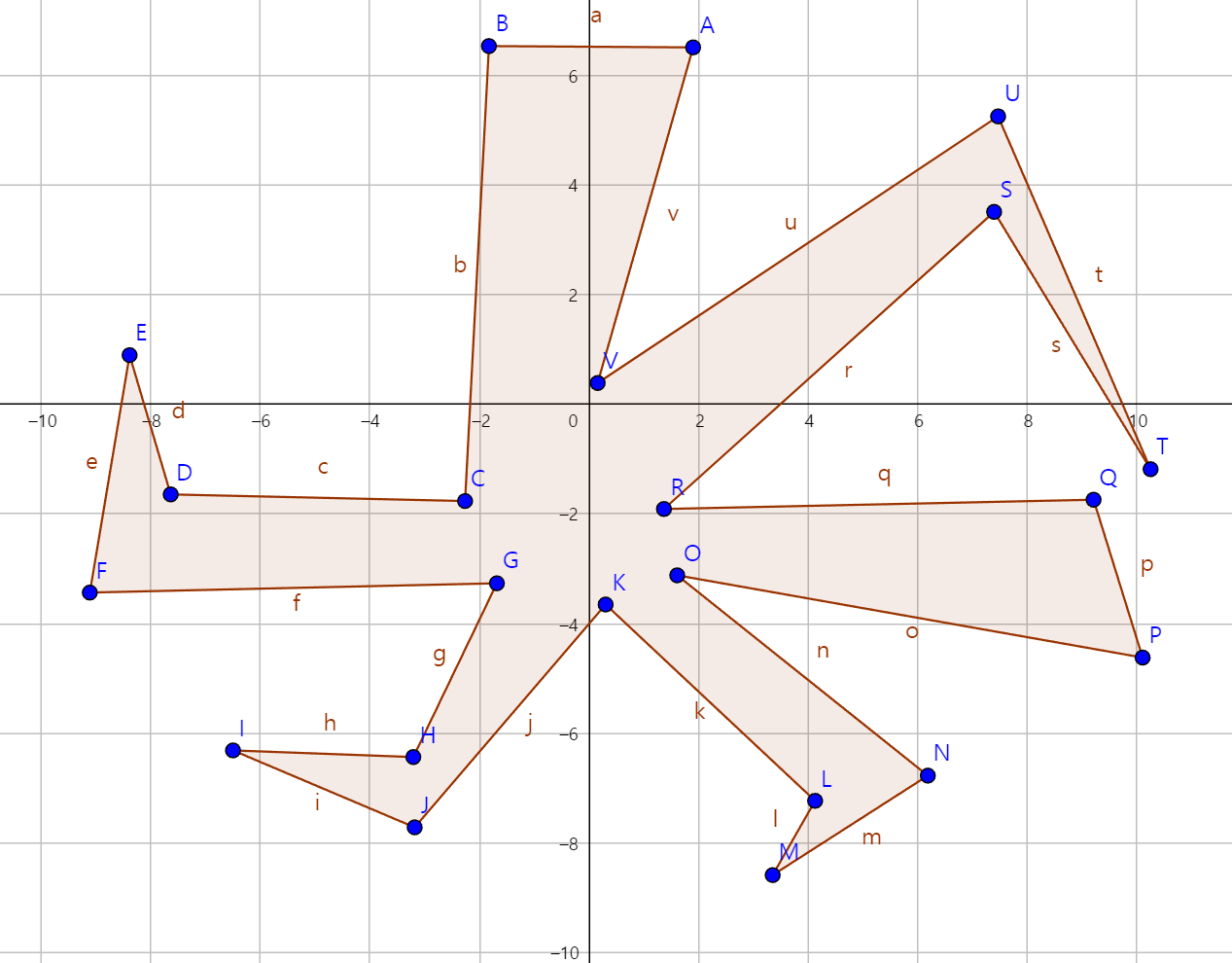
여기서 $A$에서 도달할 수 있는 영역부터 계산해 보기로 하자. 일단 $A$에서 $B$로 간다. 그리고 $B$에서 $C$로 간다. 이 때, $A, B, C$ 순서대로 보면 반시계방향이니 문제가 없다. 그다음에 $C$에서 $D$로 가는 경우를 보자. 이런 경우에는 $B,C,D$를 보면 시계방향으로 회전해버린다. 반대로말하면, $D$에서 $B$를 갈 때는 무조건 반시계방향으로 한 번 회전해야 한다는 뜻이다. 따라서 저 $D$쪽으로는 갈 수 없다. 그러니 그냥 $\overrightarrow{BC}$방향으로 쭉 간다. 그러면 $\overline{FG}$에 부딪힌다. 그러면 $\overline{FG}$에 부딪힌 교점을 $F_2$라 하자. 그러면 도형은 원래 $ABCDEFGHIJKLMNOPQRSTUV$순으로 그려져 있었는데 $ABCF_2GHIJKLMNOPQRSTUV$가 된 것이다.

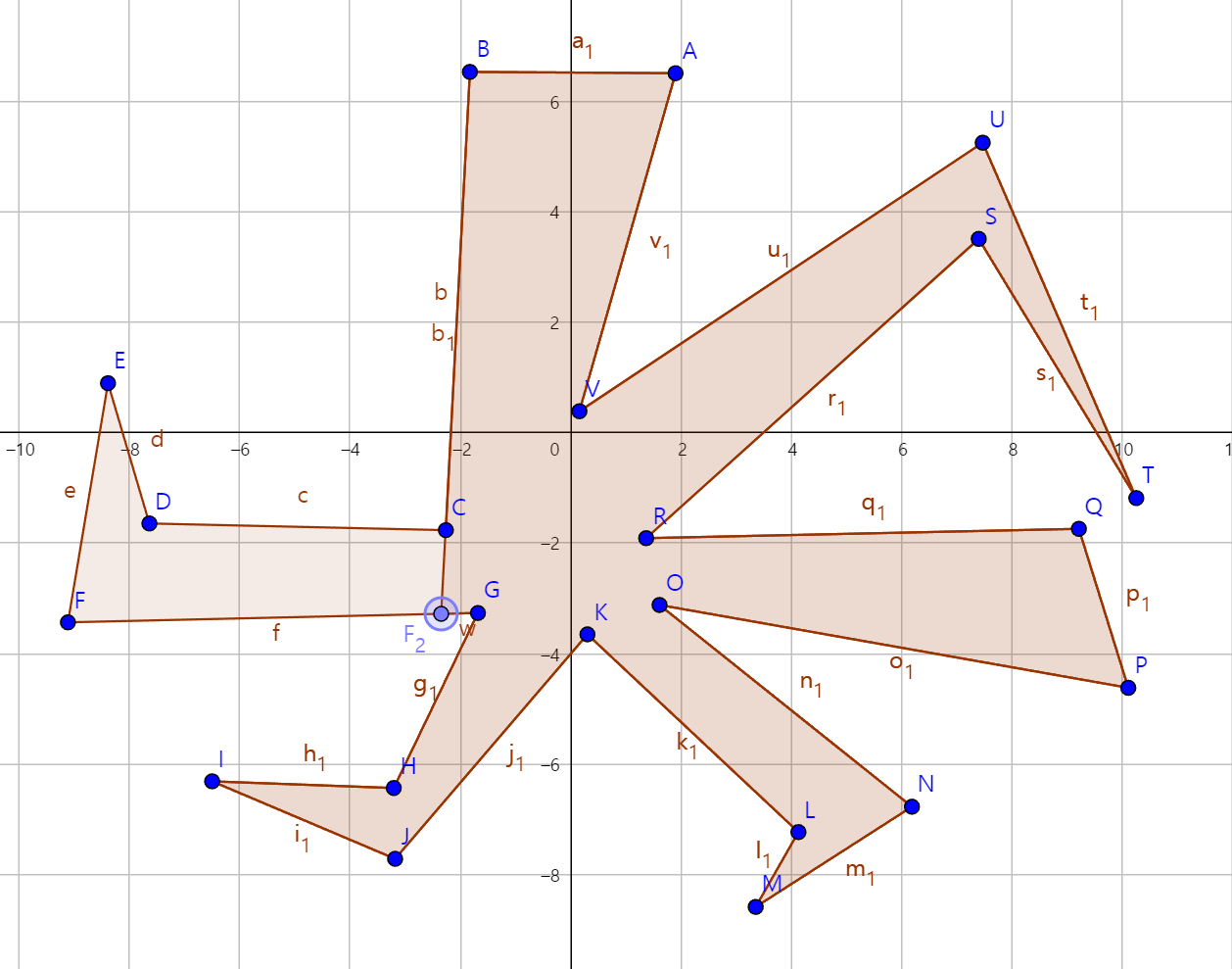
이런 식으로 되는 것이다. 이제 $F_2$부터 이어서 비슷한 방식으로 해 보자. $CF_2G$는 반시계방향이므로 그냥 간다. $F_2GH$는 시계방향이므로 $\overrightarrow{F_2G}$를 그려서 교차하는 점을 찾는다. 그 다음에는... 이런식으로 $V$까지 진행했다고 가정하자. 그러면 다음과 같은 그림이 될 것이다.

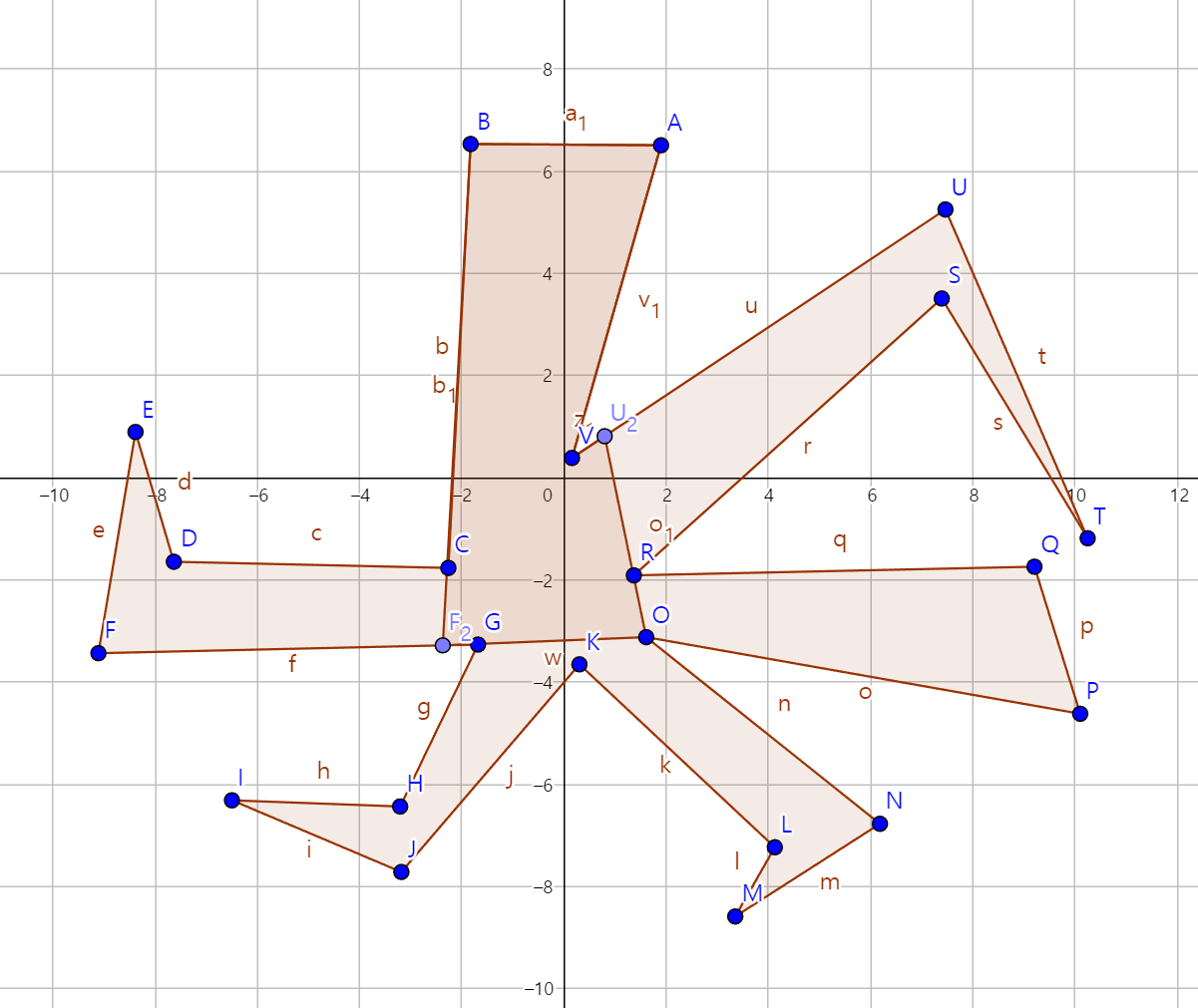
이제 여기서 $U_2VA$는 시계방향이므로 $\overrightarrow{U_2V}$와 교차하는 곳을 찾아야 하는데, 이는 $\overline{BF_2}$이다. $\overline{BC}$도 마찬가지로 교차하긴 하지만, (((우리는 새로 만들고 있는 도형인 $ABF_2GOU_2V$에서 교차하는 것만 보기로 한다.))) 그러면 $\overrightarrow{U_2V}$와 $\overline{BF_2}$가 교차하는 점을 $B_2$라 하자. 그런데 $B$는 이미 한번 방문했었다. 즉, 하나의 도형이 만들어 진 것이다.

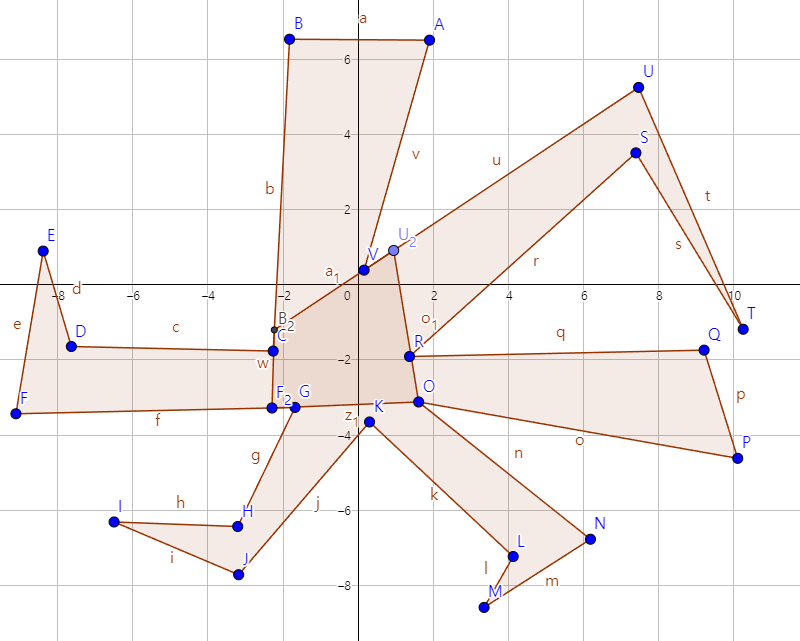
이렇게 $U_2B_2F_2O$의 볼록다각형이 만들어졌다. 볼록다각형인 이유는 반시계방향으로만 회전했으니 당연하다. 그런데 사실 이렇게 구한 도형의 영역은 $A$에서 반시계방향으로 갈 수 있는 모든 영역이 아니다. 예를 들면 $A$에서 $N$까지 반시계방향으로만 꺾으면서 충분히 갈 수 있다.

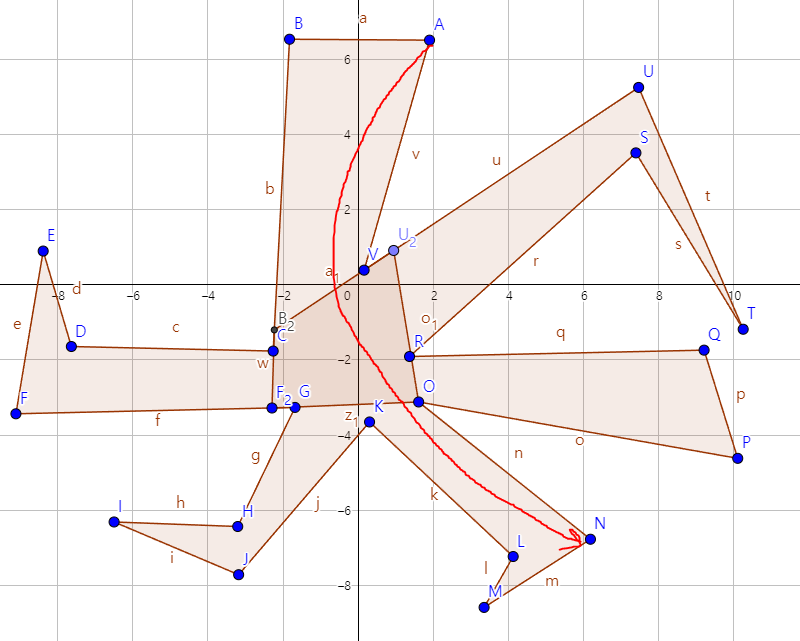
하지만 이 문제의 최종 목적은 한 점이 아닌 모든 점에서 도달할 수 있는 영역을 구해야 한다. 우리는 위에서 $F_2GH$는 시계방향이기 때문에 무시하고 $\overrightarrow{F_2G}$와 교차하는 지점을 신경썼는데, 이 과정에서 $F$가 가지 못하는 영역을 신경써 버린 것이다. 실제로 $F$에서 $N$까지 가는 데 반시계방향만으로 꺾어서 갈 수 있는 방법은 없다.이제 여기서 원래 주어진 다각형을 $D_1$, 우리가 이를 잘라내서 만드는 중인 다각형을 $D_2$라 하자. 그러면 이제 $D_1$의 다른 점들에 대해서도 방금 전과 마찬가지로 다 해보면 된다. 여기서 그냥 $D_2$의 점에 대해서만 해 보면 된다고 생각할 수 있는데 안된다. 이는 문제 예제에도 잘 나와있다.

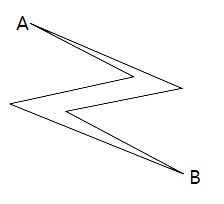
여기서 $A$에서 시작하는 영역이랑 $B$에서 시작하는 영역이랑 교차하는 부분은 없기 때문에 재미있는 점의 영역은 아예 존재하지 않는다. 그런데 $A$에서 갈수있는 영역을 먼저 잘라내면 이렇게 될 것이다.

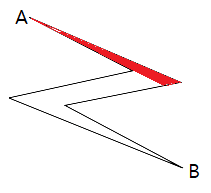
이 영역은 사실 $B$에서는 절대 가지 못하기 때문에 $B$를 무시하면 안된다.