https://www.acmicpc.net/problem/12772

이 문제는 두 simple polygon을 이리저리 회전시키고 이동시켜서 접선의 길이의 합을 최대로 한 값을 구하는 것이다. 단, 두 도형이 서로 겹치면 안된다.

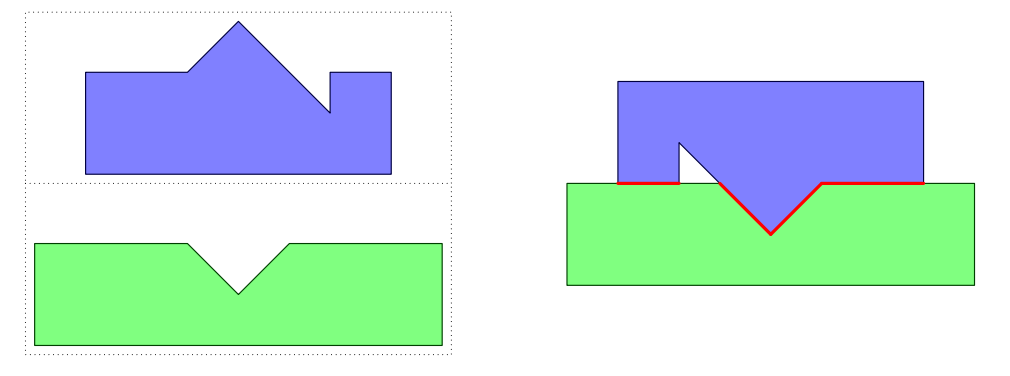
이런 경우는 쉬워 보이지만

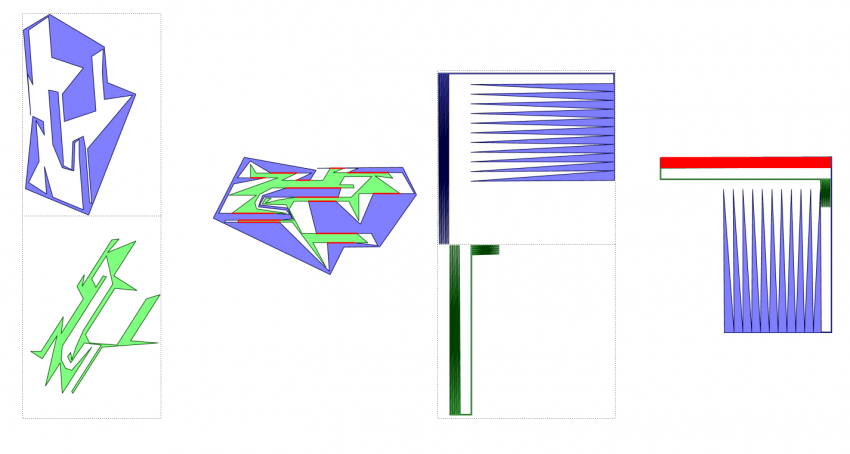
이런 경우 어떻게 구할지 막막할 것이다.그런데 자세히 보면 두 도형의 꼭짓점 개수는 각각 최대 50개이다. 그리고 시간제한은 20초이다. 따져보면 시간복잡도가 $o(n^5 log n)$이어도 괜찮다.($50^5 * log_2 50 \leq 1875000000$)

이렇게 생각해 보니 뭔가 다 해보면 될 것 같다는 느낌이 들었다. 그리고 그 예상은 맞았다. 물론 다해본다고 해도 무식하게 도형을 0.00..0001도씩 회전시켜 보면서 $10^{-4}$만큼 x,y방향으로 각각 이동시켜보면 너무 많은 연산을 하기 때문에 시간초과일 것이다. ($10^{-4}$만큼 움직인다고 한 이유는 문제에서 입력 데이터는 꼭짓점이 최대 $10^{-7}$ 만큼 이동하더라도 답이 $10^{-4}$이상 증가하지 않도록 선택되었다고 했기 때문이다.)

그런데 이 문제는 접선의 길이의 합을 최대로 한 값을 구하는 문제이다. 적어도 도형 A의 선분과 도형 B의 선분이 적어도 1개는 아주 조그마한 길이라도 겹쳐야 한다. (정확히는 이렇지 않은 케이스도 있다. 아예 A와 B의 공통된 접선 자체가 없을 때가 있는데, 이럴 경우에는 최대 길이는 당연히 0이다.) 이러면 굳이 하나씩 회전하고 움직일 필요 없이 A의 변 하나와 B의 변 하나를 골라서, 이 둘이 닿아있는 모든 경우를 계산해보면 된다. 여기서 두 변을 $l_a, l_b$라 하겠다. 둘이 평행하지 않을 경우에는 당연히 A와 B 둘 중 한 도형을 회전시켜서 서로 평행하게 만들어 주어야 한다.(여기서는 A는 고정시켜두고 B를 회전, 이동한다고 하겠다.) 그런데 이렇게 해도 아직 시간이 오래 걸린다. 조금 더 줄여보자. $l_a, l_b$ 둘이 닿아있는 모든 경우를 계산해 볼 필요는 없다. 중요한 것은 A를 고정시켜놓고 B를 $l_a, l_b$와 평행하게 움직이다가, B와 A가 서로 닿아서 못움직이는 곳이 있을 것이다.

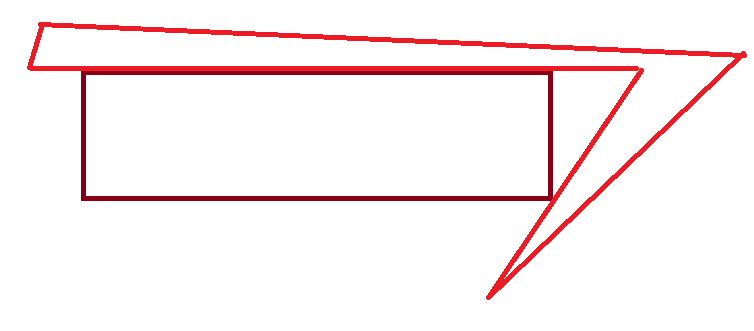
예를 들면 A : 빨간색 도형, B : 갈색 직사각형 이라고 하면, B는 여기서 더 오른쪽으로 움직일 수 없다.그리고 각 꼭짓점의 위치와 $l_a, l_b$가 수직인 부분에서도 멈춰야 한다.

예를 들면 이런 경우에도 멈춰야 한다는 뜻이다.

이렇게 움직이다가 움직임을 멈춰야 하는 특정 위치, 그리고 각 꼭짓점의 위치와 $l_a, l_b$와 수직인 부분에서 멈추기만 하면 된다. 이런 특정 위치만 계산해 봐도 되는 이유를 설명하겠다. 최댓값을 달성하려면, 어느 방향으로도 아주 미세하게라도 움직일 수 없어야 한다. 움직일 수 있다면 더 늘어날 가능성이 있기 때문이다.

마지막으로, 이렇게 해 본 상태에서 추가로 A와 B가 서로 겹치는지도 확인해 봐야 한다.

지금까지 한 것을 시간복잡도 분석해 보면, A와 B의 각각 변을 하나씩 겹쳐보는 데는 $O(n^2)$, 두 도형의 위치 개수는$O(n)$, A와 B가 겹치는지 확인하는 데는 $O(n^2)$, 총 $O(n^5)$라 할 수 있다. (여기서는 A의 꼭짓점 개수 = B의 꼭짓점 개수 = $n$으로 두었다.) $50^5 = 312500000$이니 시간초과가 나지 않을 것이다.

그런데 최적화를 잘 못해서 시간이 훨씬 오래 걸렸다..

여기서 한가지 더 생각해보면 도형 겹치는지 검사하는 데는 $O(n^2)$이 걸렸다고 했는데, 사실 샤모스-호이 라는 알고리즘을 사용하면 $O(nlogn)$에 할 수 있다. 나중에 이 문제 시간 더 최적화 할 때는 한번 해 보려 한다.